- Published on
梯度消失和BN
梯度消失
产生梯度消失的前提:
- 基于梯度的训练方法
- 激活函数输出值范围小于输入值范围
梯度消失的原因,如图双曲正切函数tanh将负无穷大到正无穷大的输入压缩到-1,1之间,当输入值较大或较小时,梯度非常接近0,导致该结点系数的变化对网络的输出影响极小,造成训练的困难
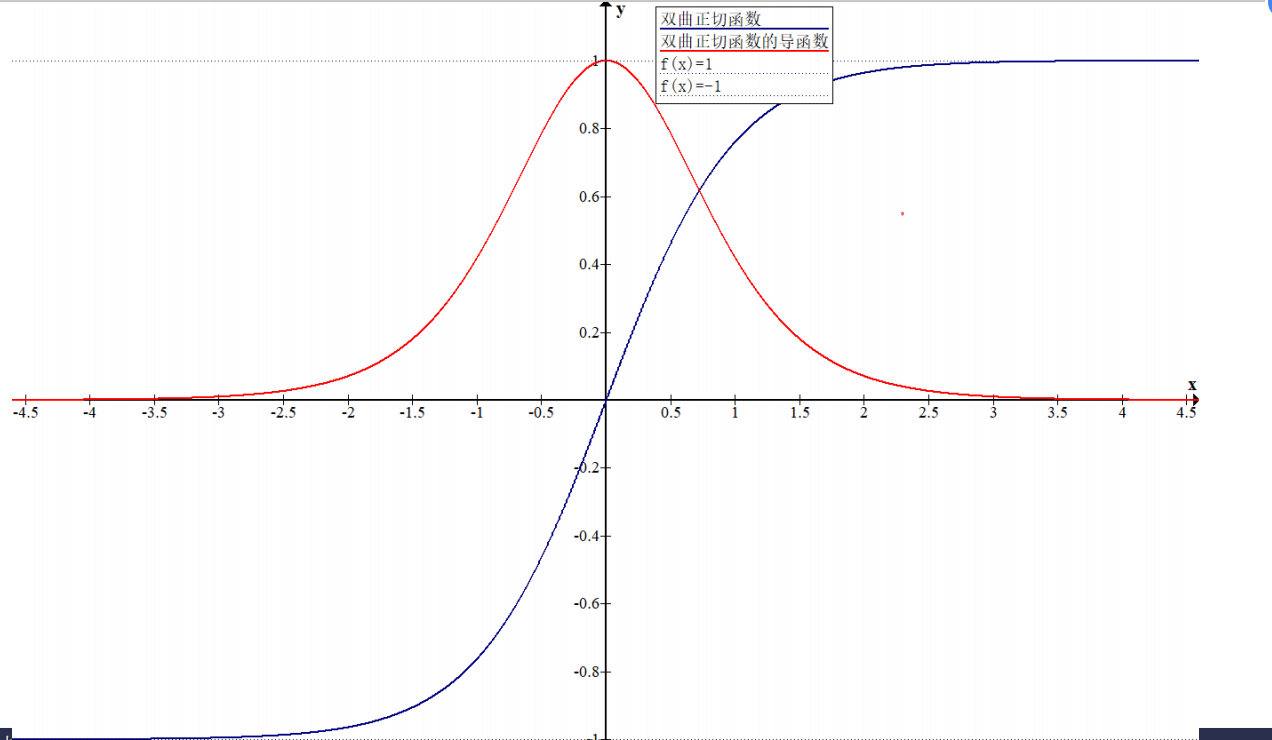
Gradient Vanishing解决方案:
- 激活函数ReLu$f(x)=max(0,x)$,输入大于0,梯度为1,否则为0。LeakyReLu:$f(x)=max(ax,x)$,输入大于等于0,梯度为1,否则为a
ReLu在零点不可导,所以在ReLu在反向传播函数实现中,将ReLu在零点位置的导数设置为0
- 使用BN,例如在sigmoid激活函数里面,将数据归一化到(0,1)之间,可以防止值较大时,梯度为0。
- 采用不使用梯度的网络训练方法。
- 基于遗传,进化算法
- 粒子群优化
- 使用残差网络结构,减少梯度传播的路径长度
- 在RNN网络中,使用LSTM减轻梯度消失。
Normalization BN/LN/WN
Covariate shift问题:
-
convariate shift 其实就是条件概率p(y|x)相同,边缘概率p(x)不同的一个偏移。也就是神经网络每层之间无法满足独立同分布。
这里面的边缘概率代表的就是某一样本x出现的概率,条件概率代表的是某一样本x出现且这一样本属于某一类y的概率。
假设训练数据和测试数据是满足相同分布的,那么训练数据训练的模型在测试数据上就能够获得很好的效果。
ICS会导致哪些问题:
- 上层参数需要不断适应新的输入数据分布,降低学习速度
- 训练过程中,随着网络加深,整体分布逐渐往激活函数的饱和区间移动,从而反向传播时出现梯度消失,也就是收敛变得很慢。(点乘运算的无界性导致)
- 每层的更新都会影响到其他层。
normalization基本思想:
要解决独立同分布的问题,理论上我们对于每一层进行白化操作,但是标准的白化操作代价很高,并且在网络中还要保证我们的操作是可导的,可以通过反向传播来更新梯度。
这里我们采用Normalization方式,但是均值方差一致并不说明就是相同的分布了,normalizaiton并不是直接解决ICS问题,更多的是面向梯度消失,和加速收敛的。类似covariance shift比较直接的解决思路应该是,通过学习训练集和测试机的分布对样本附加权重,来学习最终的模型。



https://blog.csdn.net/zxyhhjs2017/article/details/79405591
所以Normalizaiton只是将x映射到一个确定的区间范围而已。
Normalization的通用公式:
$$ h=f(g\cdot\frac{x-\mu}{\sigma}+b)
$$
$\mu$平移参数,$\sigma$是缩放参数,通过shift和scale变换得到均值为0,方差为1的标准分布,(这步规范化将数据映射到激活函数的线性区,会降低神经网络的表达能力,所以需要进行下一步的变换)
g再平移参数,b再缩放参数,得到一个均值为b,方差为$g^2$的分布
BN

BN针对每个样本x的单个维度$x_i$,计算大小为m的mini-batch的均值和方差。
BN是对一个batch进行一阶统计量和二阶统计量的计算,这就要求每个batch之间,以及整体数据应该是近似同分布的。如果每个batch之间的分布差异较大,那么每个batch就是进行不一样的数据变换,所以我们应该尽可能的调大batch的数量和shuffle数据。每一层进行标准化,同时还需要保存统计量,占用内存大。
LN
BN是对单个维度进行标准化,而LN则是对所有维度同时进行标准化,这就需要注意不同维度对应的特征的关系,假如各个维度表示的特征的纲量不一致(比如颜色和大小),那么会导致模型的表达能力下降。
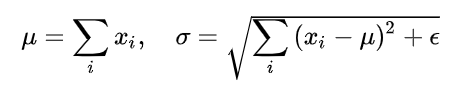
WN
https://zhuanlan.zhihu.com/p/3317324


CN-Cosine Normalization
向量的点积是无界的(权重向量w和数据x),向量点积是衡量两个向量相似度的方法之一。同样的夹角余弦也可以这这样做。并且夹角余弦的取值范围是[-1,1],所以我们可以改变线性变换的函数为:
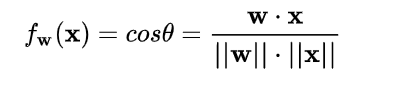
CN再WN的基础上,scale加上了向量的模
Normalization为什么有效
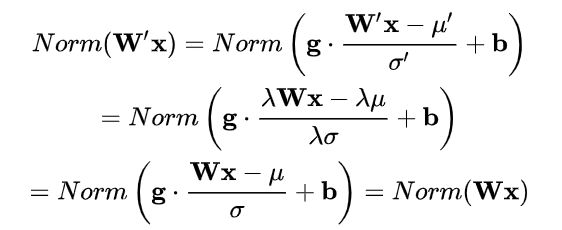
权重的伸缩变化不会影响反向梯度的 Jacobian 矩阵,因此也就对反向传播没有影响**,避免了反向传播时因为权重过大或过小导致的梯度消失或梯度爆炸问题**,从而加速了神经网络的训练。
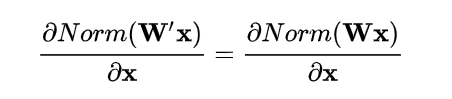
权重伸缩不变性还有参数正则化的效果:下层的权重值越大,梯度就越小($1/\lambda$),参数变化稳定,实现了正则化的效果,可以使用更高的学习率,避免参数大幅震荡,提高网络的泛化能力。
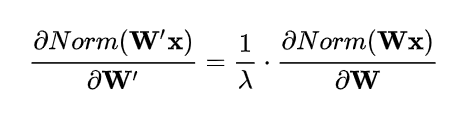
- 数据伸缩性不变
数据伸缩性对BN,LN,CN成立,三者对输入数据进行规范化,分子分母相互抵消。所以不管底层的数据如何变化,对于一层神经元来说,输入始终保持标准的分布。使得训练过程更加鲁棒。