HMM_参数估计

HMM基本概念

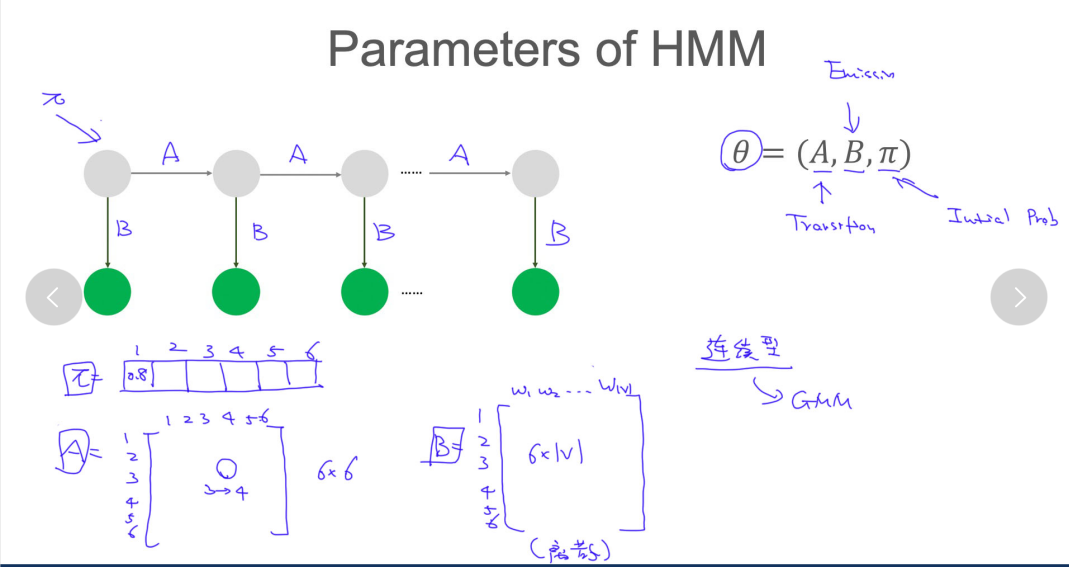
参数

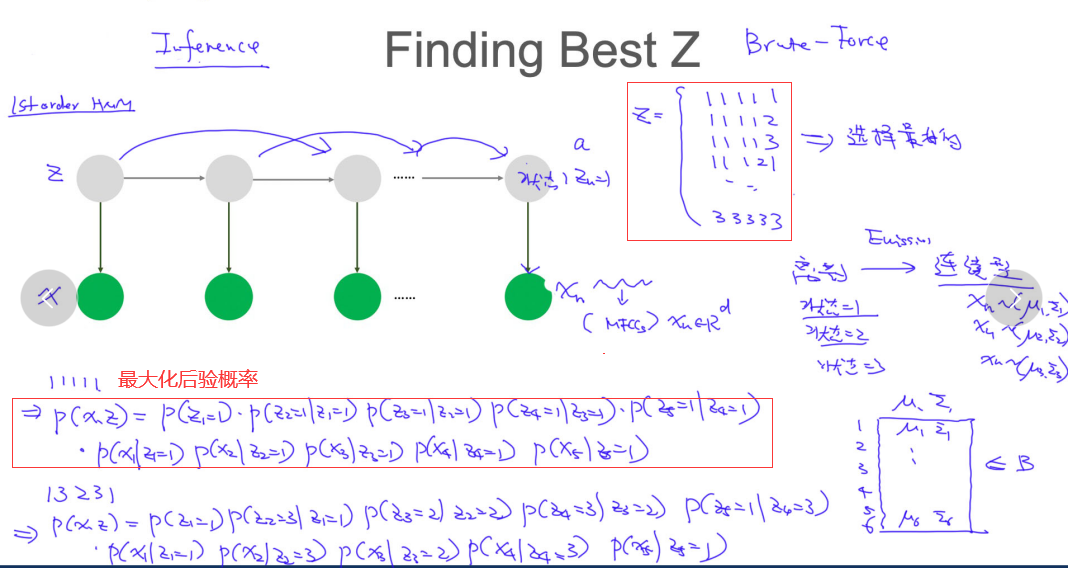
Two Major Tasks

1. 给定模型的参数，找到最适合的z inference
2. 估计模型的参数 $\theta$ parameter estimator

Inference

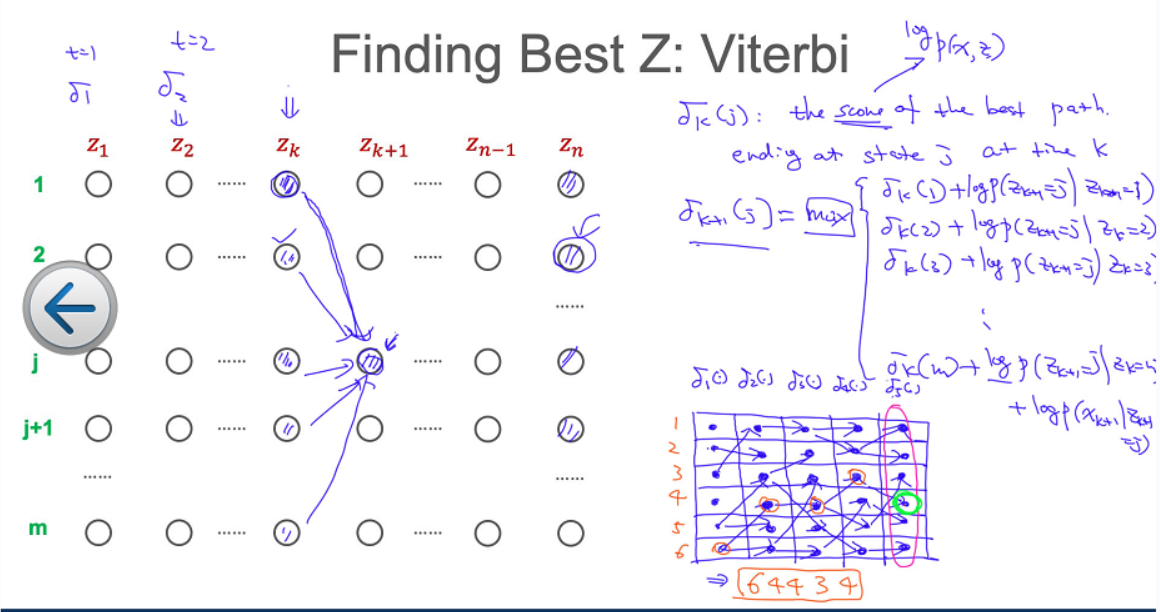
使用暴力的求解方法：

找到所有z的组合，然后求后验概率p(z|x)

P(z|x)后验概率，这里求的是P(z,x)，原理上是一样的

P(z|x) = P(z,x) / P(x) P(x)是归一化项，都是一样的，而且计算P(x)会很难，这里我们只需要找到最大的后验概率，所以只需要求P(z|x)

动态规化算法

Viterbi算法。见黄皮笔记本2切

参数估计

Complete Case

已知 x，z 估计参数

z三个状态： 1 2 3

估计A：归一化 按照每一行

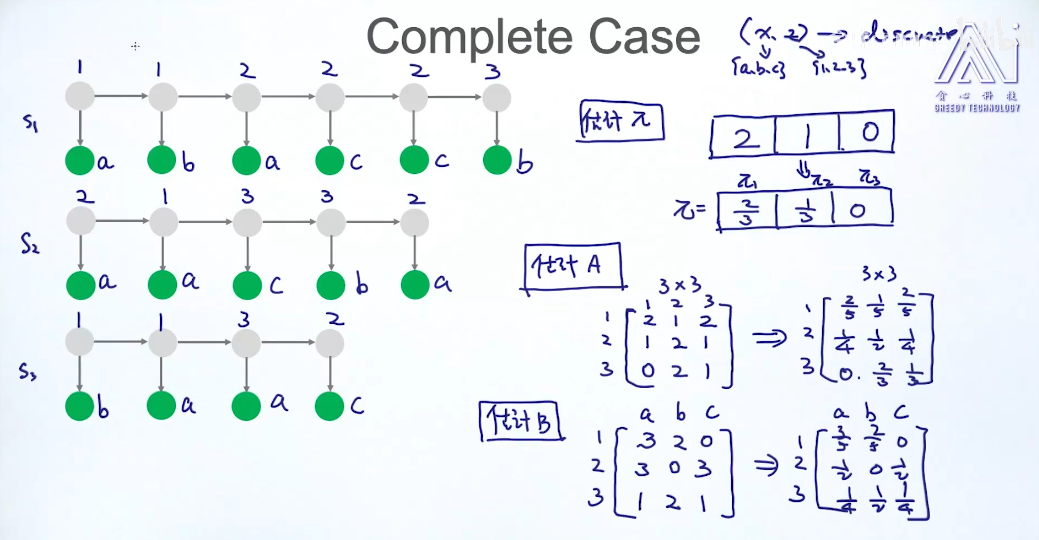
Incomplete Case

z的状态数目是提前定义好的，超参数

F/B算法，计算 $p(z_k|x)$,可以求出z的期望

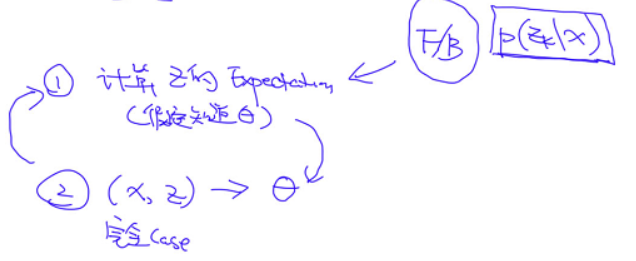
EM算法

1. 计算z的exception，通过F/B算法 P(z_K|x)
2. 通过(x,z) 求 theta，complete case

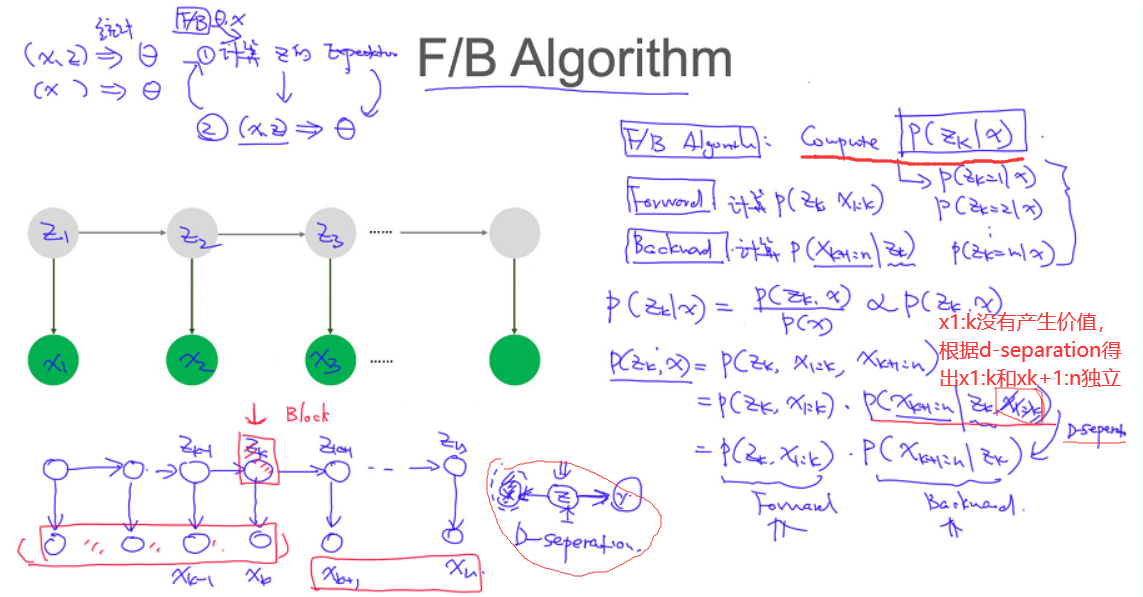
FB算法 F，B动态规划概率公式问题

1. 首先根据动态规划算法的公式要求，写出等式
2. 判断左边变量是否在右边出现过
3. 对于未出现的变量，通过概率边缘化添加
4. 通过P(AB) = P(A|B)P(B)来进行公式求解
5. 最终解式要往$z_k$,$x_k$,$x_k+1,z_k+1$上凑，从而使用发射矩阵，和转移矩阵表示结果。（给定$x和\theta$）

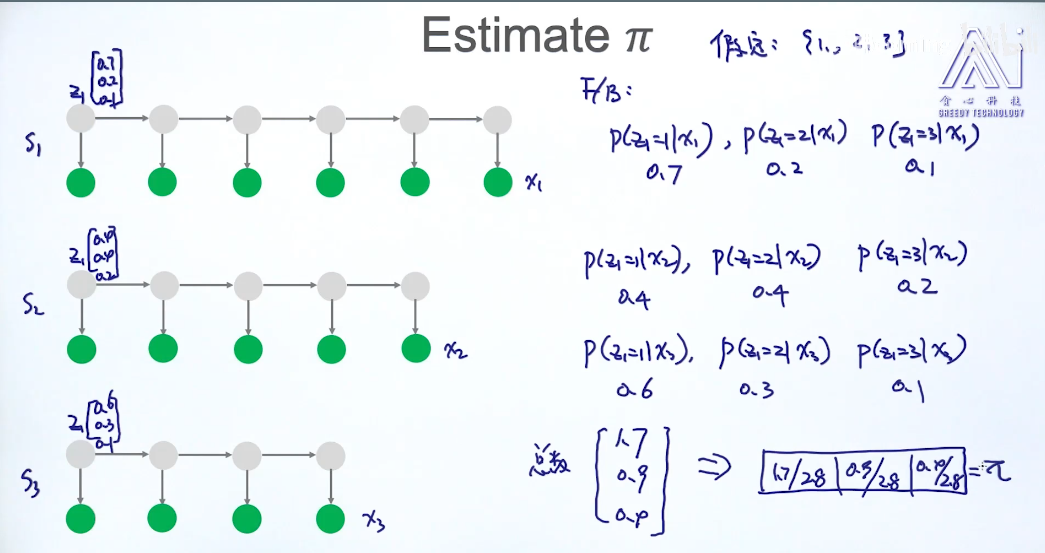
估计PI

我们通关F/B算法可以求出$P(z_k|x)$

假设有三个状态：我们可以计算

针对不同的样本x: $P(z_1|x)，P(z_2|x)，P(z_3|x)$ 看作为次数，将所有的次数相加，再归一化得到概率。

估计B

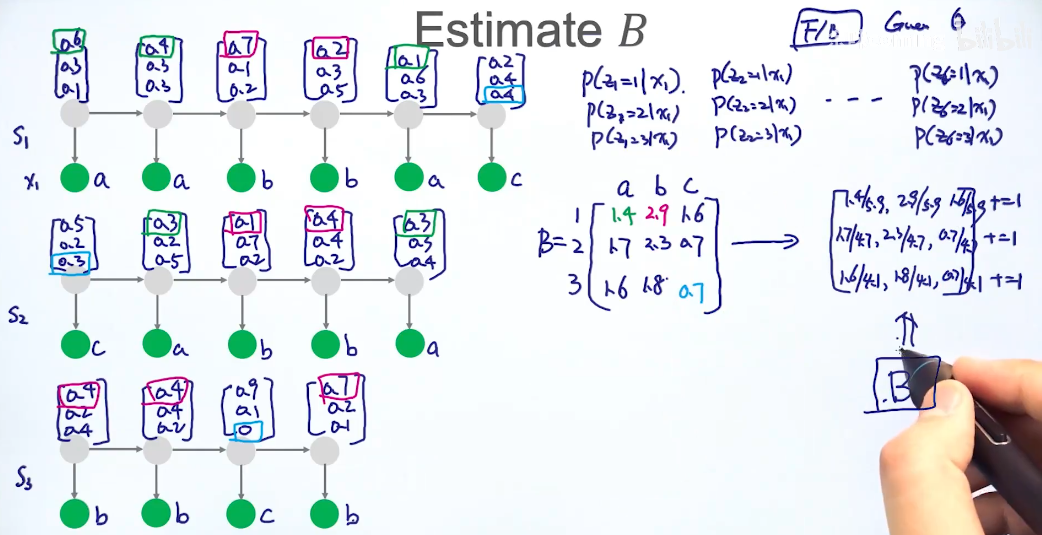
估计A

计算A稍微复杂，A是一个状态转移矩阵

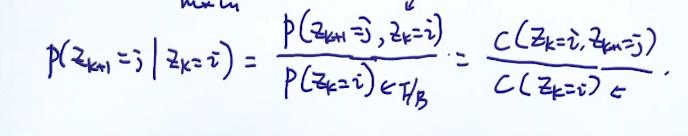
求解会涉及到条件概率，通过对公式的转化，最后需要求解一个联合概率。

estimate A 具体步骤