Reinforcement_Learning

Shusen Wang

基础

Probalility Density Function-PDF

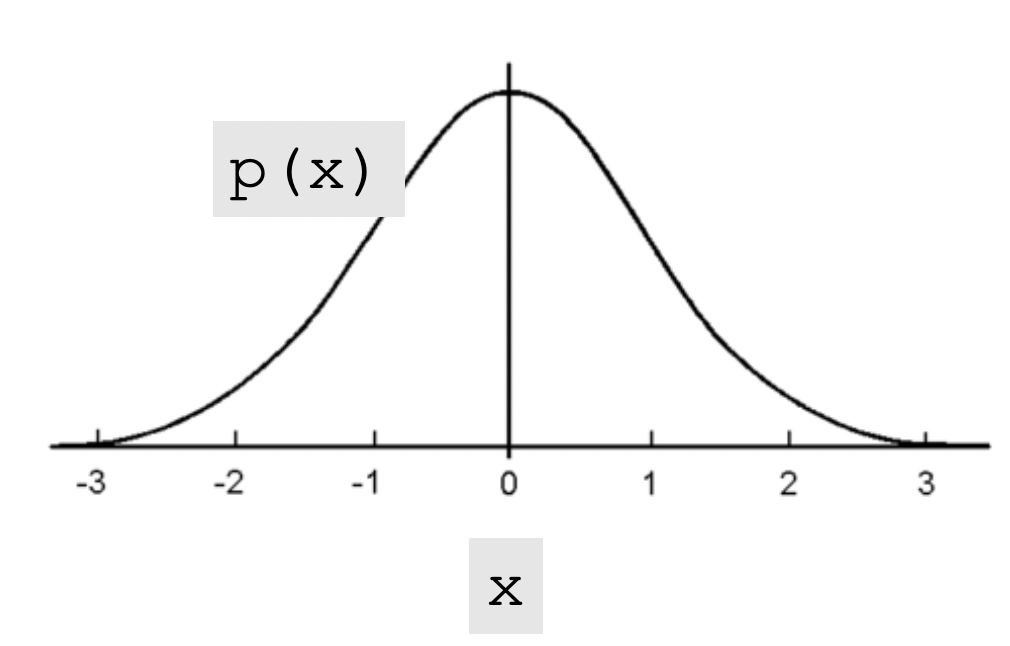
高斯分布：$p(x)=\frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left(-\frac{(x-\mu)^2}{2 \sigma^2}\right)$

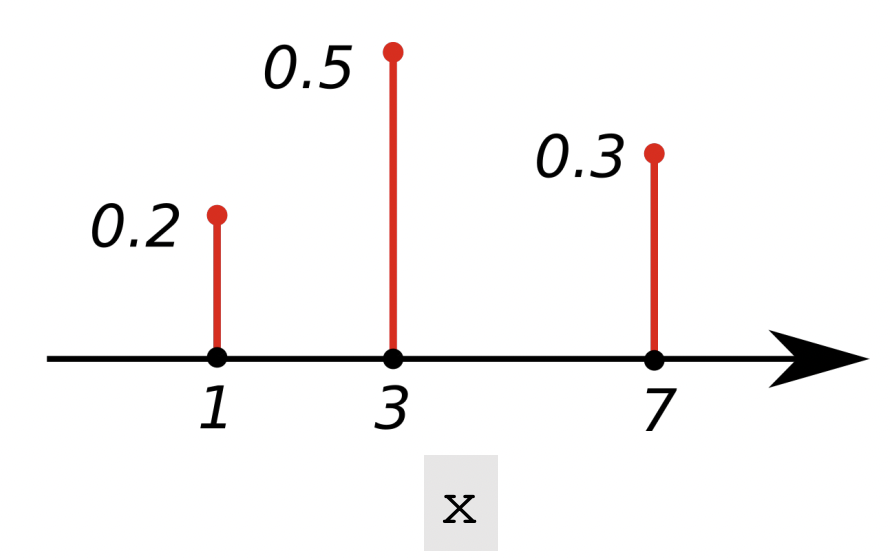
离散分布

PDF：$p(1)=0.2, p(3)=0.5, p(7)=0.3$

对于连续分布：

$\int_x p(x) d x=1$

对于离散分布：

$\sum_{x \in x} p(x)=1$

Expectation

对于随机变量X，

连续分布的期望为：$\mathbb{E}[f(X)]=\int_x p(x) \cdot f(x) d x$

离散分布的期望为：$\mathbb{E}[f(X)]=\sum_{x \in X} p(x) \cdot f(x)$

术语

状态： state 行为： action 策略： policy 奖赏： reward

状态转移：state transition

对于马里奥游戏 ：

$s$ state: 游戏中的一帧图片。

$a$action: 马里奥可以左，右，跳三个动作。 所以$a \in{$ left, right, up $}$

$\boldsymbol{\pi}$policy function:策略函数，根据当前的state选择最好的action。$\pi(a \mid s)=\mathbb{P}(A=a \mid S=s)$

$R$Reward:吃一个金币，或赢得游戏。赢得游戏的奖赏大于吃一个金币。触碰到Goomba则奖赏为负数，上述所有情况都没发生则奖赏为0.

state transition:

随机性

策略函数是一个概率函数。 所以每次的action都是随机的。

$A \sim \pi(\cdot \mid s)$

old state 根据action转变到new state。$S^{\prime} \sim p(\cdot \mid s, a)$状态也是随机的。

定义

交互行为：

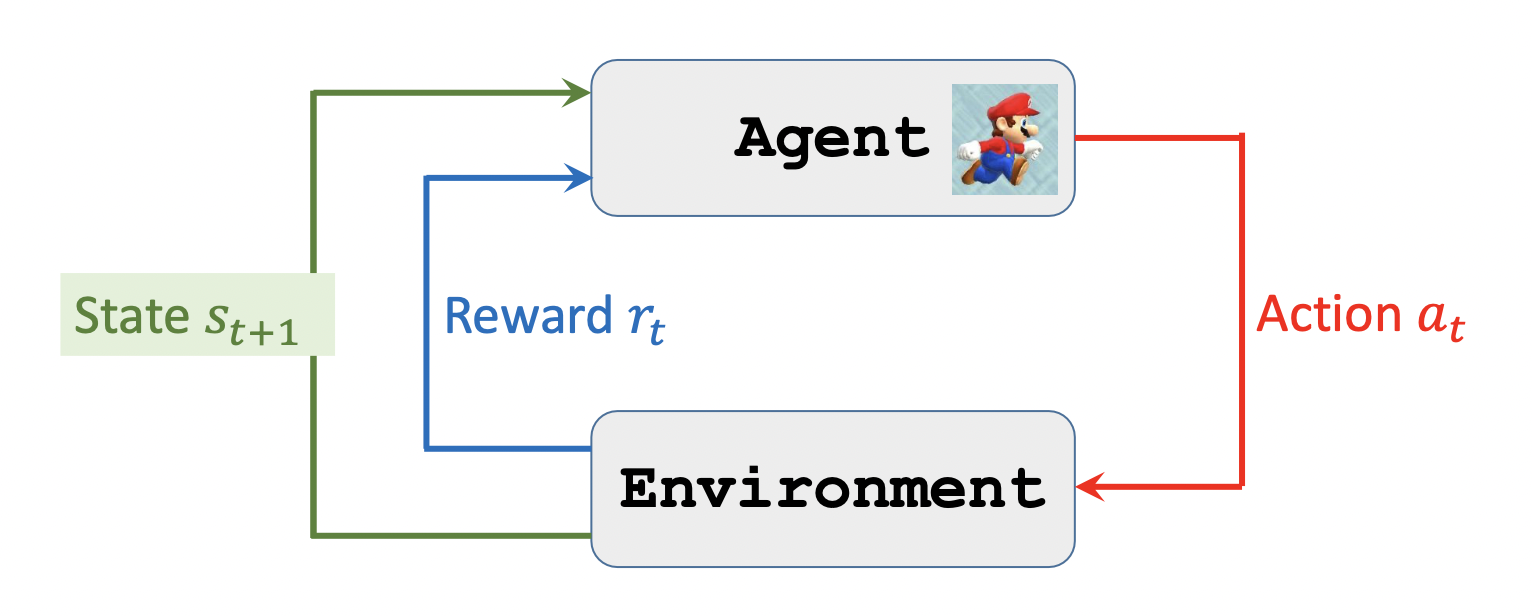
根据当前state和policy function选择一个action

action会产生一个新的state和Reward

一个好的policy function可以产生更多的奖励。根据奖励可以指导policy function。

Definition ： Return 累计未来奖励(cumulative future reward)。

$U_t=R_t+R_{t+1}+R_{t+2}+R_{t+3}+\cdots$

未来奖励权重要低于当下奖励的权重

Definition：Discounted return

$\gamma$:discount factor(超参数)

$U_t=R_t+\gamma R_{t+1}+\gamma^2 R_{t+2}+\gamma^3 R_{t+3}+\cdots$随机的，R依赖于s，a。 s，a是随机的。

Definition： Action-Value Function 为动作A打分。当前动作好不好

$Q_\pi\left(s_t, a_t\right)=\mathbb{E}\left[U_t \mid S_t=s_t, A_t=a_t\right]$条件期望

$U_t$依赖于$S_t,S_{t+1},...,S_n$和$A_t,A_{t+1},...,A_n$

$s_t,a_t$是观测变量，$s_{t+1},...,S_n$和$A_{t+1},...,A_n$是随机变量

Actions are random：$\mathbb{P}[A=a \mid S=s]=\pi(a \mid s)$ policy function

State are random：$\mathbb{P}\left[S^{\prime}=s^{\prime} \mid S=s, A=a\right]=p\left(s^{\prime} \mid s, a\right)$ state function

Ut也是随机变量。

可以对$U_t$这个随机变量求期望。将里面的随机性积掉，可以得到一个实数。比如我们知道抛硬币的正面朝上的概率是0.5， 正面朝上记为1，反面为0，则期望为0.5。

除了$s_t,a_t$未来的动作状态都被积掉了，$s_t，a_t$被作为观测到的数值替代而不是随机变量。Q还与policy function有关，如果policy函数不一样则$Q_\pi$也不一样，已知policy函数，$Q_\pi$就会为当前状态下所有的a打分。

Definition： Optimal action-value function

$Q^{\star}\left(s_t, a_t\right)=\max \pi Q\pi\left(s_t, a_t\right)$去掉policy function。最优动作价值函数

Definition：State-value function

$V_\pi\left(s_t\right)=\mathbb{E}A\left[Q\pi\left(s_t, A\right)\right]=\sum_a \pi\left(a \mid s_t\right) \cdot Q_\pi\left(s_t, a\right)$当Aciton是离散的时候。

描述当前状态S好不好。

可以把动作A作为随机变量，对A求期望 A的概率密度函数是$\underline{A} \sim \pi\left(\cdot \mid s_t\right)$.，把A消掉。求期望得到的$V_\pi$只和$\pi$和s有关。如果$\pi$是固定的，那么状态越好，$V_\pi$的值越大。

如果$\pi$越好，则$\mathbb{E}S\left[V\pi(S)\right]$ $V_\pi(S)$的期望就越大。